[프로그래머스] 배달 / Swift

[문제 보기]

N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

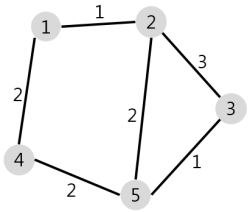
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.

제한사항

• 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
• road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
• road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
• road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
  • a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
  • 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
  • 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
• K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
• 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
• 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.

---

입출력 예

N, road, K, result

5	[[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]]	3	4
6	[[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]]	4	4

입출력 예 설명

입출력 예 #1
문제의 예시와 같습니다.

 

입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.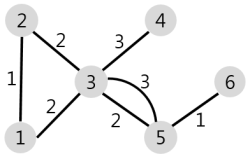

1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.

 

https://programmers.co.kr/learn/courses/30/lessons/12978

코딩테스트 연습 - 배달

 

---

다익스트라 알고리즘을 사용하여 풀었다.

 

import Foundation

func solution(_ N:Int, _ road:[[Int]], _ k:Int) -> Int {
    
    let INF = 987654321
    // 입력받은 값으로 그래프 초기화
    var graph = [[(to: Int, cost: Int)]](repeating: [], count: N+1)
    for element in road {
        if let beforeSavedIndex1 = graph[element[0]].firstIndex(where: { $0.to == element[1] }),
           let beforeSavedIndex2 = graph[element[1]].firstIndex(where: { $0.to == element[0] }) {
            let beforeSaved = graph[element[0]][beforeSavedIndex1]
            if beforeSaved.cost > element[2] { // 이전에 저장된 값보다 작을 경우
                graph[element[0]][beforeSavedIndex1] = (to: element[1], cost: element[2])
                graph[element[1]][beforeSavedIndex2] = (to: element[0], cost: element[2])
            }
        } else {
            graph[element[0]].append((to: element[1], cost: element[2]))
            graph[element[1]].append((to: element[0], cost: element[2]))
        }
    }
    
    var visited = [Bool](repeating: false, count: N+1)
    var distance = [Int](repeating: INF, count: N+1)
    
    func getSmallestNode() -> Int {
        var minValue = INF
        var index = 0
        for i in (1..<N+1) {
            if !visited[i], distance[i] < minValue {
                    index = i
                    minValue = distance[i]
            }
        }
        return index
    }
    
    func dijkstra(_ start: Int) {
        // 시작노드에 대해서 초기화
        visited[start] = true
        distance[start] = 0 // 자기자신은 0
        for element in graph[start] {
            distance[element.to] = element.cost
        }
        
        for _ in (0..<N-1) {
            let now = getSmallestNode() // 최단 거리가 짧은 노드를 하나꺼내고 방문 처리함
            visited[now] = true
            // 현재 노드에 연결된 모든 노드들에 대해서
            // 현재 노드까지 오는데 걸리는 비용과 간선값의 합과 이웃노드에 적힌 값을 비교함
            for element in graph[now] {
                let cost = distance[now] + element.cost
                if cost < distance[element.to] {
                    distance[element.to] = cost
                }
            }
        }
    }
    
    dijkstra(1)
    
    return distance[1...].filter { $0 <= k }.count
}